2.2: Tangent och derivata
Centralt innehåll
Begreppet gränsvärde. Begreppen sekant, tangent, förändringshastighet, ändringskvot och derivata för en funktion. Grafiska och digitala metoder för att derivera funktioner. Villkor för deriverbarhet.
En tangent är en rät linje som tangerar en funktionsgraf i en punkt. Derivata beskriver tangentens lutning och motsvarar en hastighet vid just det tillfället. Denna kan bestämmas via s.k. derivatafunktioner. Varje polynom har ett annat polynom med 1 gradtal lägre som derivatafunktion.
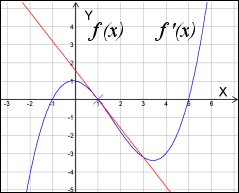
| Här introduceras begreppen derivata och tangent, och de första deriveringsreglerna tas fram. | Exempel på hur man deriverar med digitala verktyg |
|---|
Skriftlig version (.pdf) (.notebook)
Slumpade grafer med frågor om f ' och f
Slumpade grafer med frågor av typen f '(2) + f(-1)
Slumpade derivatagrafer (från "mor till dotter")
Slumpade derivatagrafer (från "dotter till mor")
Diagnos (version 1)(version 2)(version 3) +
Facit (version 1)(version 2)(version 3)
